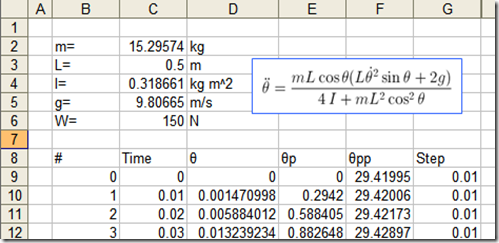
Consider an Excel sheet to solve the compound pendulum equation numerically
The equation itself does not matter. What is important is that the angular acceleration depends on the angle and the angular speed (as well as possibly time).
The values m, L, g etc. are constants and can be declared as named ranges (for example cell C2 contains the value for m and is declared with the name "m").
I setup a row on Excel with the initial conditions, and the calculation above in a formula as the last cell in the row. For each calculation row, the position and velocity is calculated using a VBA script and called from the Excel sheet
| Row | Time (C) | θ (D) | θp (E) | θpp (F) | Step (G) |
| 9 | 0 | 0 | 0 | =L*m*COS(D9)*(L*E9^2*SIN(D9)+2*g)/(4*I+m*L^2*COS(D9)^2) | 0.02 |
| 10 | =C9+G9 | =RK4STEPX(G9,C9,D9,E9,F9) | =RK4STEPV(G9,C9,D9,E9,F9) | =L*m*COS(D10)*(L*E10^2*SIN(D10)+2*g)/(4*I+m*L^2*COS(D10)^2) | 0.02 |
| 11 | =C10+G10 | =RK4STEPX(G10,C10,D10,E10,F10) | =RK4STEPV(G10,C10,D10,E10,F10) | =L*m*COS(D11)*(L*E11^2*SIN(D11)+2*g)/(4*I+m*L^2*COS(D11)^2) | 0.02 |
The trick now is to pass into RK4STEPX and RK4STEPV the formula for θpp instead of the value. To do so the function declaration is
Public Function Rk4StepX(ByVal h As Double, ByVal t As Double, ByVal q As Double, ByVal qp As Double, ByRef qpp As Range) As Double
...
End Function
If you notice that qpp is passed by reference as a range the formula can be extracted by qpp.FormulaR1C1. In fact the magic actually happens in a different function tasked with evaluating the acceleration based on given position and velocity (and time).
Public Function CalcAcc(ByVal t As Double, ByVal q As Double, ByVal qp As Double, ByRef qpp As Range) As Double
Dim f As String
f = Mid(qpp.FormulaR1C1, 2)
f = Replace(f, "RC[-3]", CStr(t))
f = Replace(f, "RC[-2]", CStr(q))
f = Replace(f, "RC[-1]", CStr(qp))
CalcAcc = qpp.Worksheet.Evaluate(f)
End Function
To explain the code, the cell range containing the acceleration formula is passed in qpp. The formula is extracted in f as a string, with the leading "=" removed. The the value in the 3rd column to the left "RC[-3]" is replaced by the given value of time, the 3nd column to the left "RC[-2]" with position, and the column to the left "RC[-1]" with velocity. Lastly, the function string is evaluated on the worksheet where any named ranges exist. The expression will result in a number if the cell it corresponds resolves to a number in the worksheet.
Now that the acceleration function is defined in VBA, implementing the Runge-Kutta scheme is trivial, except this is a 2nd order ODE and the typical scheme for 1st order ODE is adapted by the author.
So here is the code that advances the position and velocity in its entirety.
Public Function Rk4StepX(ByVal h As Double, ByVal t As Double, ByVal q As Double, ByVal qp As Double, ByRef qpp As Range) As Double
Dim K0 As Double, K1 As Double, K2 As Double, K3 As Double
Dim Q0 As Double, Q1 As Double, Q2 As Double, Q3 As Double
Dim h2 As Double, h6 As Double, a As Double
h2 = h / 2: h6 = h / 6
a = qpp.Value2
Q0 = qp + h2 * a
K0 = CalcAcc(t + h2, q + h2 * qp, Q0, qpp)
Q1 = qp + h2 * K0
K1 = CalcAcc(t + h2, q + h2 * Q0, Q1, qpp)
Q2 = qp + h2 * K1
K2 = CalcAcc(t + h, q + h * Q1, Q2, qpp)
Rk4StepX = q + h * (qp + h6 * (a + K0 + K1))
End Function
Public Function Rk4StepV(ByVal h As Double, ByVal t As Double, ByVal q As Double, ByVal qp As Double, ByRef qpp As Range) As Double
Dim K0 As Double, K1 As Double, K2 As Double, K3 As Double
Dim Q0 As Double, Q1 As Double, Q2 As Double, Q3 As Double
Dim h2 As Double, h6 As Double, a As Double
h2 = h / 2: h6 = h / 6
a = qpp.Value2
Q0 = qp + h2 * a
K0 = CalcAcc(t + h2, q + h2 * qp, Q0, qpp)
Q1 = qp + h2 * K0
K1 = CalcAcc(t + h2, q + h2 * Q0, Q1, qpp)
Q2 = qp + h2 * K1
K2 = CalcAcc(t + h, q + h * Q1, Q2, qpp)
Rk4StepV = qp + h6 * (a + 2 * K0 + 2 * K1 + K2)
End Function
The results are graphed (in Excel) and shown below